1、排序
1.1 冒泡排序 Bubble Sort
原理:冒泡排序大概的意思是依次比较相邻的两个数,然后根据大小做出排序,直至最后两位数。由于在排序过程中总是小数往前放,大数往后放,相当于气泡往上升,所以称作冒泡排序。代码实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
function BubbleSort($arr) {
if (!is_array($arr) || empty($arr)) {
return $arr;
}
$len = count($arr);
for ($i = 0; $i < $len - 1; $i++) {
for($j= 0; $j < $len - $i - 1; $j++) {
if ($arr[$j] > $arr[j+1]) {
$temp = $arr[$j + 1];
$arr[$j + 1] = $arr[$j];
$arr[$j] = $temp;
}
}
}
return $arr;
}
|
1.2 选择排序 Selection sort
原理:首先在未排序序列中找到最小元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小元素,然后放到排序序列末尾。以此类推,直到所有元素均排序完毕。
示例代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| function selectSort($arr) {
if(!is_array($arr) || empty($arr)) {
return $arr;
}
$len = count($arr);
for ($i=0; $i < $len - 1; $i++) {
$p = $i;
for ($j=$i + 1; $j < $len; $j++) {
$p = ($arr[$p] <= $arr[$j]) ? $p:$j;
}
if ($p != $i) {
$tmp = $arr[$p];
$arr[$p] = $arr[$i];
$arr[$i] = $tmp;
}
}
return $arr;
}
|
1.3 插入排序 Insert Sort
原理:
通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。插入排序在实现上,通常采用in-place排序(即只需用到O(1)的额外空间的排序),因而在从后向前扫描过程中,需要反复把已排序元素逐步向后挪位,为最新元素提供插入空间。
步骤:
1 从第一个元素开始,该元素可以认为已经被排序
2 取出下一个元素,在已经排序的元素序列中从后向前扫描
3 如果该元素(已排序)大于新元素,将该元素移到下一位置
4 重复步骤3,直到找到已排序的元素小于或者等于新元素的位置
5 将新元素插入到该位置中
6 重复步骤2
示例代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
function insertSort($arr) {
if(!is_array($arr) || empty($arr)) {
return $arr;
}
$len = count($arr);
for ($i = 1; $i < $len; $i++) {
$tmp = $arr[$i];
for ($j = $i - 1; $j >= 0; $j--) {
if ($tmp < $arr[$j]) {
$arr[$j + 1] = $arr[$j];
$arr[$j] = $tmp;
} else {
break;
}
}
}
return $arr;
}
|
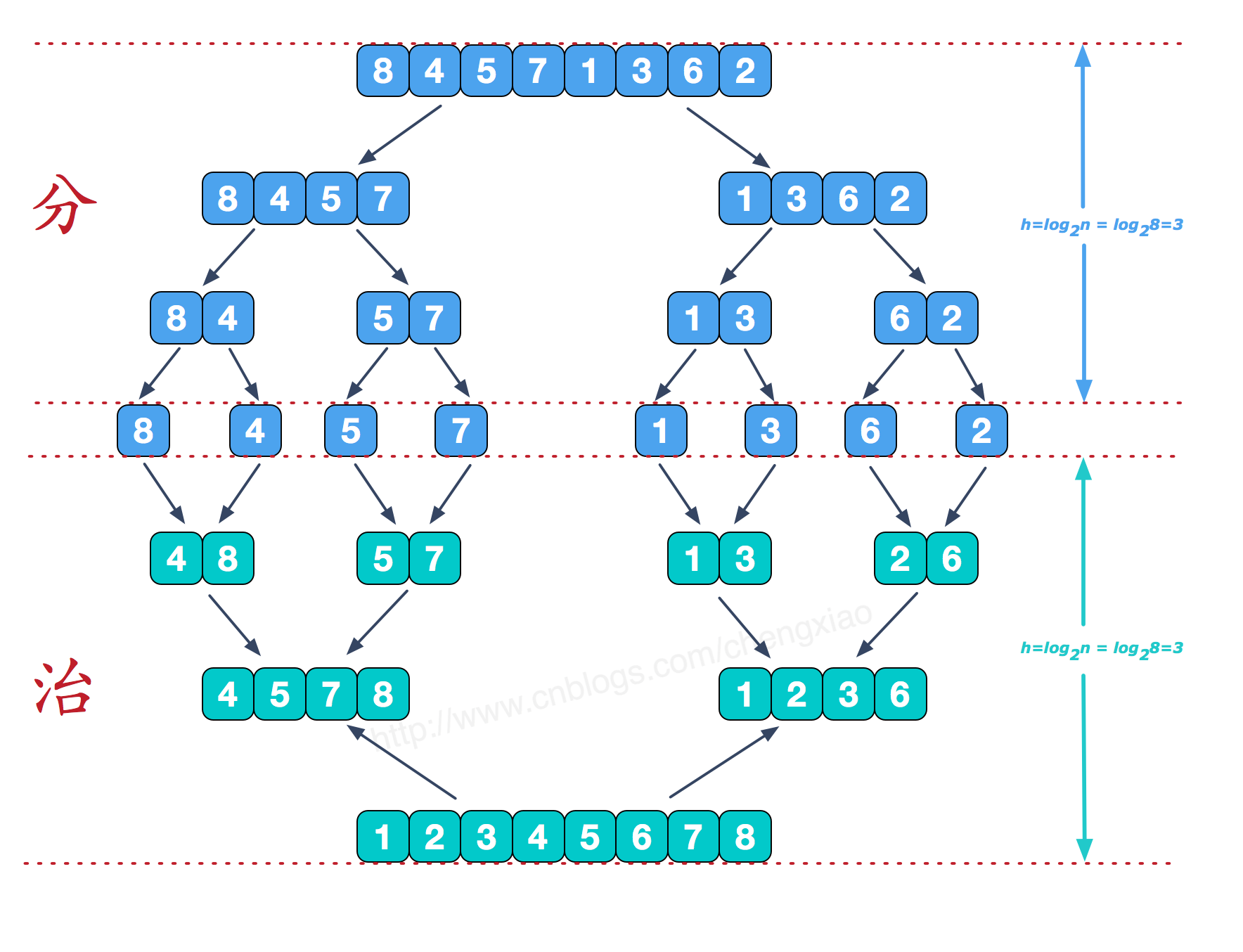
1.4 归并排序
原理:
利用递归,先拆分、后合并、再排序。
步骤:
1 均分数列为两个子数列
2 递归重复上一步骤,直到子数列只有一个元素
3 父数列合并两个子数列并排序,递归返回数列
示例代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| function mergeSort($arr) {
if(!is_array($arr) || empty($arr)) {
return $arr;
}
$len = count($arr);
if ($len <= 1) {
return $arr;
}
$mid = intval($len / 2);
$left = array_slice($arr, 0, $mid);
$right = array_slice($arr, $mid);
$left = mergeSort($left);
$right = mergeSort($right);
return merge($left, $right);
}
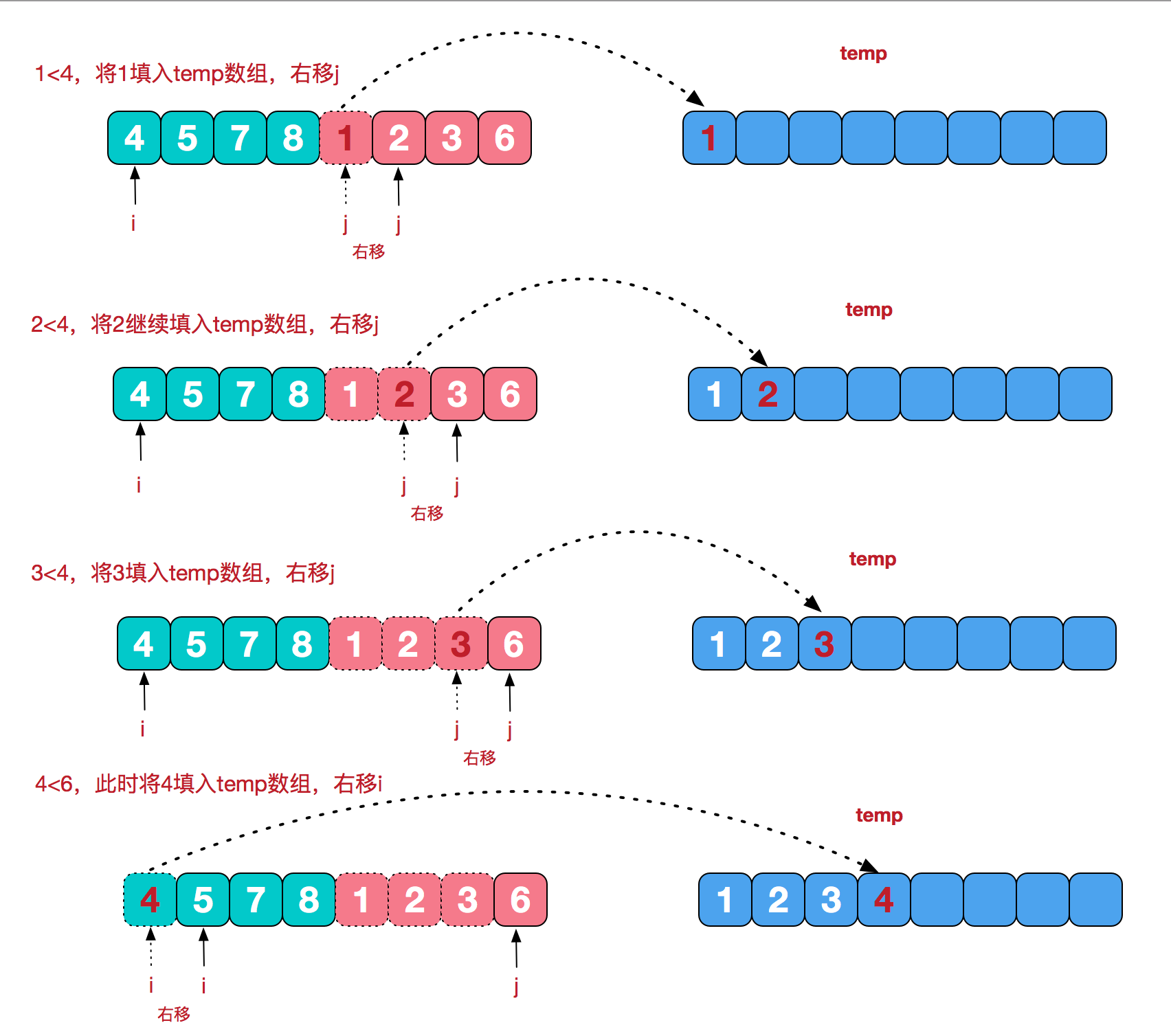
function merge($arrA, $arrB) {
$arrC = [];
while(count($arrA) && count($arrB)) {
$arrC[] = $arrA[0] < $arrB[0] ? array_shift($arrA) : array_shift($arrB);
}
return array_merge($arrC, $arrA, $arrB);
}
|
图示:

1.5 快速排序 Quick Sort
快速排序是由东尼·霍尔所发展的一种排序算法。
原理:
在平均状况下,排序 n 个项目要Ο(n log n)次比较。在最坏状况下则需要Ο(n2)次比较,但这种状况并不常见。事实上,快速排序通常明显比其他Ο(n log n) 算法更快,因为它的内部循环(inner loop)可以在大部分的架构上很有效率地被实现出来,且在大部分真实世界的数据,可以决定设计的选择,减少所需时间的二次方项之可能性。
步骤:
1 从数列中挑出一个元素,称为 “基准”(pivot)
2 重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作
3 递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。
示例代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| function quickSort($arr) {
if (!is_array($arr)) {
return $arr;
}
$len = count($arr);
if ($len <= 1) {
return $arr;
}
$left = [];
$right = [];
for ($i = 1; $i < $len; $i++) {
if ($arr[$i] < $arr[0]) {
$left[] = $arr[$i];
} else {
$right[] = $arr[$i];
}
}
$left = quickSort($left);
$right = quickSort($right);
return array_merge($left, [$arr[0]], $right);
}
|
1.6 希尔排序 Shell Sort
希尔排序属于插入类排序,是将整个有序序列分割成若干个小的子序列分别进行插入排序。
排序过程:先取一个正整数d1<n,把所有序号相隔d1的数组元素放一组,组内进行直接插入排序,然后取d2<d1,重复上述分组和排序操作,直至d1=1,即所有记录放进一个组中排序为止。(将每间隔一定步距的数取出来进行比较,比如gap=5,就是把第1个、第6个、第11个…数取出来进行插入排序)
优点:
当n值很大时,数据项每一趟排序需要移动的个数很少,但数据项的距离很长;当n值减小时,每一趟需要移动的数据增多,此时已经接近于它们排序后的最终位置。
示例代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
function shellSort($arr)
{
$count = count($arr);
$inc = $count;
do {
$inc = ceil($inc / 2);
for ($i = $inc; $i < $count; $i++) {
$temp = $arr[$i];
for ($j = $i - $inc; $j >= 0 && $arr[$j + $inc] < $arr[$j]; $j -= $inc) {
$arr[$j + $inc] = $arr[$j];
}
$arr[$j + $inc] = $temp;
}
} while ($inc > 1);
return $arr;
}
|
2 搜索
2.1 二分查找 Binary Search
原理:
首先,将表中间位置记录的值与查找值比较,如果两者相等,则查找成功;否则利用中间位置将表分成前、后两个子表,如果中间位置的值大于查找值,则进一步查找前一子表,否则进一步查找后一子表。
重复以上过程,直到找到满足条件的记录,使查找成功,或直到子表不存在为止,此时查找不成功。
步骤:
- 将数组的第一个位置设置为下边界(0)。
- 将数组最后一个元素所在的位置设置为上边界(数组的长度减 1)。
- 若下边界等于或小于上边界,则做如下操作:
a. 将中点设置为floor((上边界+下边界)/2)。
b. 如果中点的元素小于查询的值,则将下边界设置为中点元素所在下标加1。
c. 如果中点的元素大于查询的值,则将上边界设置为中点元素所在下标减1。
d. 否则中点元素即为要查找的数据,可以进行返回。
示例代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
|
function binarySearch($arr, $res) {
$right = count($arr);
$left = 0;
while($left <= $right) {
$middle = floor(($right + $left) / 2);
if (!isset($arr[$middle])) {
return -1;
}
if ($arr[$middle] == $res) {
return $middle;
}
if ($arr[$middle] < $res) {
$left = $middle + 1;
} else {
$right = $middle - 1;
}
}
return -1;
}
function binarySearch2($arr, $search) {
if (empty($arr)) {
return -1;
}
$low = 0;
$high = count($arr) - 1;
while ($low <= $high) {
$mid = intval(($high - $low) / 2) + $low;
$val = $arr[$mid];
if ($search == $val) {
return $mid;
} elseif ($search < $val) {
$high = $mid - 1;
} else {
$low = $mid + 1;
}
}
return -1;
}
|



